SHAP (SHapley Additive exPlanations)
This chapter is currently only available in this web version. ebook and print will follow.
SHAP (SHapley Additive exPlanations)
룬드버그와 리(2016)의 SHAP(SHapley Additive ExPlanations)1는 개별 예측을 설명하는 방법이다. SHAP는 이론적으로 최적의 Shapley Values 게임을 기반으로 한다.
SHAP가 독자적인 장을 얻었고 Shapley values의 부제가 아닌 두 가지 이유가 있다. 첫째, SHAP 저자들은 현지 대리모형에서 영감을 받은 샤플리 값에 대한 대체 커널 기반 추정 접근방식인 커널SHAP를 제안했다. 그리고 그들은 트리 기반 모델에 대한 효율적인 추정 접근법인 TreeSHAP를 제안했다. 둘째, SHAP에는 샤플리 값의 집계에 기초한 많은 글로벌 해석 방법이 포함되어 있다. 이 장에서는 새로운 추정 접근법과 글로벌 해석 방법을 모두 설명한다.
Shapley values와 local models (LIME)의 장을 먼저 읽어 보는 것이 좋다.
정의
SHAP의 목표는 예측에 대한 각 형상의 기여도를 계산하여 인스턴스 x의 예측을 설명하는 것이다. SHAP 설명법은 탄전 게임 이론에서 샤플리 값을 계산한다. 데이터 인스턴스의 특징 값은 연합에서 플레이어 역할을 한다. 샤플리 값은 형상들 사이에 “지불” (= 예측)을 공정하게 분배하는 방법을 알려준다. 플레이어는 예를 들어 표 형식의 데이터를 위한 개별 기능 값이 될 수 있다. 플레이어는 피쳐 값의 그룹도 될 수 있다. 예를 들어, 이미지를 설명하기 위해 픽셀을 슈퍼 픽셀로 그룹화할 수 있고 그 사이에 분포할 수 있다. SHAP가 표에 제시하는 한 가지 혁신은 샤플리 값 설명이 선형 모델인 적층 특성 귀속 방법으로 표현된다는 것이다. 그 견해는 LIME과 Shapley Values를 연결한다. SHAP는 설명을 다음과 같이 명시한다.
\[g(z')=\phi_0+\sum_{j=1}^M\phi_jz_j'\]여기서 g는 \(z'\in\{0,1\}^M\)는 연합 벡터, M은 최대 연합 크기, \(\phi_j\in\mathb{R}\)는 형상 j, 샤플리 값에 대한 형상 속성이다. 내가 “협약 벡터”라고 부르는 것을 SHAP 용지에서는 “간단한 특징”이라고 한다. 나는 이 이름이 선택되었다고 생각한다. 왜냐하면, 예를 들어, 이미지 데이터의 경우, 이미지는 픽셀 레벨로 표현되지 않고, 슈퍼 픽셀로 집계되기 때문이다. 나는 z가 탄약을 묘사하는 것에 대해 생각하는 것이 도움이 된다고 믿는다. 연합 벡터에서 1의 입력은 해당 형상 값이 “현재”이고 0은 “작성”임을 의미한다. 만약 당신이 샤플리의 가치에 대해 안다면 이것은 당신에게 친숙하게 들릴 것이다. 샤플리 값을 계산하기 위해 일부 형상 값만 재생되고(“현재”) 일부는 “수행”되지 않는다고 시뮬레이션한다. 연탄의 선형 모델로서의 표현은 \(\phi\)의 연산을 위한 속임수다. 관심의 인스턴스인 x의 경우, 연립 벡터 x’는 모든 1의 벡터, 즉 모든 형상 값은 “현재”이다. 이 공식은 다음을 단순화한다.
\[g(x')=\phi_0+\sum_{j=1}^M\phi_j\]이 공식은 Shapley value 장의 유사한 표기법에서 찾을 수 있다. 실제 추정에 대한 자세한 내용은 나중에 나온다. 자세한 추정을 하기 전에 먼저 \(\phi\)의 속성에 대해 이야기해보자.
샤플리 값은 효율성, 대칭, 더미 및 애드비티 특성을 충족하는 유일한 솔루션이다. 또한 SHAP는 Shapley 값을 계산하기 때문에 이러한 값을 만족시킨다. SHAP 용지에서는 SHAP 속성과 Shapley 속성의 불일치를 발견할 수 있다. SHAP는 다음과 같은 세 가지 바람직한 속성을 설명한다.
1) 로컬 정확도
\[f(x)=g(x)=\phi_0+\sum_{j=1}^M\phi_jx_j'\]\(\phi_0=E_X(\hat{f}(x)\)를 정의하고 모든 \(x_j'\)을 1로 설정하면 이것이 Shapley 효율성 속성이다. 다른 이름으로만 연합 벡터를 사용한다.
\[f(x)=\phi_0+\sum_{j=1}^M\phi_jx_j'=E_X(\hat{f}(X)+\sum_{j=1}^M\phi_j\]2) 누락
\[x_j'=0\Rightarrow\phi_j=0\]누락은 누락된 형상이 0의 속성을 갖는다고 말한다. \(x_j'\)는 결합을 의미하며, 여기서 0의 값은 형상값이 없음을 나타낸다. 연합 표기법에서 설명할 인스턴스의 모든 특성 값은 ‘1’이어야 한다. 0이 있으면 해당 인스턴스에 대해 형상 값이 누락됨을 의미한다. 이 속성은 “정상” 샤플리 값의 속성에 포함되지 않는다. 그런데 왜 우리는 그것이 SHAP에 필요한가? 룬드버그는 그것을 “소수 장부 보관 재산”)이라고 부른다. 누락된 형상은 (이론적으로) \(x_j'=0\)로 곱하기 때문에 로컬 정확도 속성을 손상시키지 않고 임의의 샤플리 값을 가질 수 있다. 결측 특성은 결측 형상이 0의 Shapley 값을 얻도록 강제한다. 실제로 이는 상수적인 특징에만 관련이 있다.
3) 일관성
\(f_x(z')=f(h_x(z')\) 및 \(z_{\setminus{}j'}\)에서 \(z_j'=0\)을 표시하도록 한다. 다음을 만족하는 두 가지 모델의 경우:
\[f_x'(z')-f_x'(z_{\setminus{}j}'\geq{}f_x(z')-f_x(z_{\setminus{}j}')\]\(z'\in\{0,1\}^M\) 입력 시:
\[\phi_j(f',x)\geq\phi_j(f,x)\]일관성 속성은 모형이 형상 값의 한계 기여도가 증가하거나 동일하게 유지되도록 변경되면(다른 형상에 관계없이) 샤플리 값도 증가하거나 동일하게 유지된다고 말한다. 일관성으로부터 Lundberg와 Lee의 부록에 설명된 대로 Shapley 특성 선형성, Dummy 및 Symmetry가 따른다.
KernelSHAP
<!- 선형모델의 일반적 아이디어 –> 커널SHAP는 예측에 대한 각 형상값의 기여도를 인스턴스(instance)에 대해 x로 추정한다. KernelSHAP는 5단계로 구성된다.
- \(z_k'\in\{0,1\}^M,\quad{}k\in\{1\ldots,K\}\) (1 = 연정에 있는 기능, 0 = 기능 없음)
- \(z_k'\)을(를) 원래 기능 공간으로 변환한 다음 f 모델 f(h_x(z_k’)를 적용하여 각 \(z_k'\)에 대한 예측을 얻으십시오.
- 각 \(z_k'\)에 대한 가중치를 SHAP 커널로 계산하십시오.
- 가중 선형 모형 적합
- Shapley 값 반환(Return Shapley)은 선형 모델의 계수(\(\phi_k\)).
우리는 0과 1의 사슬이 생길 때까지 반복해서 동전 던지기를 통해 임의의 연합을 만들 수 있다. 예를 들어, 벡터 (1,0,1,0)는 우리가 첫 번째와 세 번째 특징의 연합을 가지고 있다는 것을 의미한다. K 표본 연산은 회귀 모형의 데이터 집합이 된다. 회귀 모델의 대상은 연립에 대한 예측이다. (“잠깐만!)”이라고 하면, “모델은 이러한 2진수 연합 데이터에 대해 교육을 받지 못했고, 그들에 대해 예측을 할 수 없다.”) 기능 값의 결합에서 유효한 데이터 인스턴스로 가져오려면 \(h_x(z')=z\) 함수가 필요하며 여기서 \(h_x:\{0,1\}^M\rightrow\mathb{R}^p\). \(h_x\) 함수는 1을 설명하고자 하는 인스턴스 x의 해당 값에 매핑한다. 표 형식의 데이터의 경우, 데이터에서 샘플링하는 다른 인스턴스의 값에 0을 매핑한다. 이는 “특성 값이 없음”과 “특성 값은 데이터에서 무작위 형상 값으로 대체됨”을 동일시함을 의미한다. 표 데이터의 경우, 다음 그림은 결합에서 형상값으로의 매핑을 시각화한다.
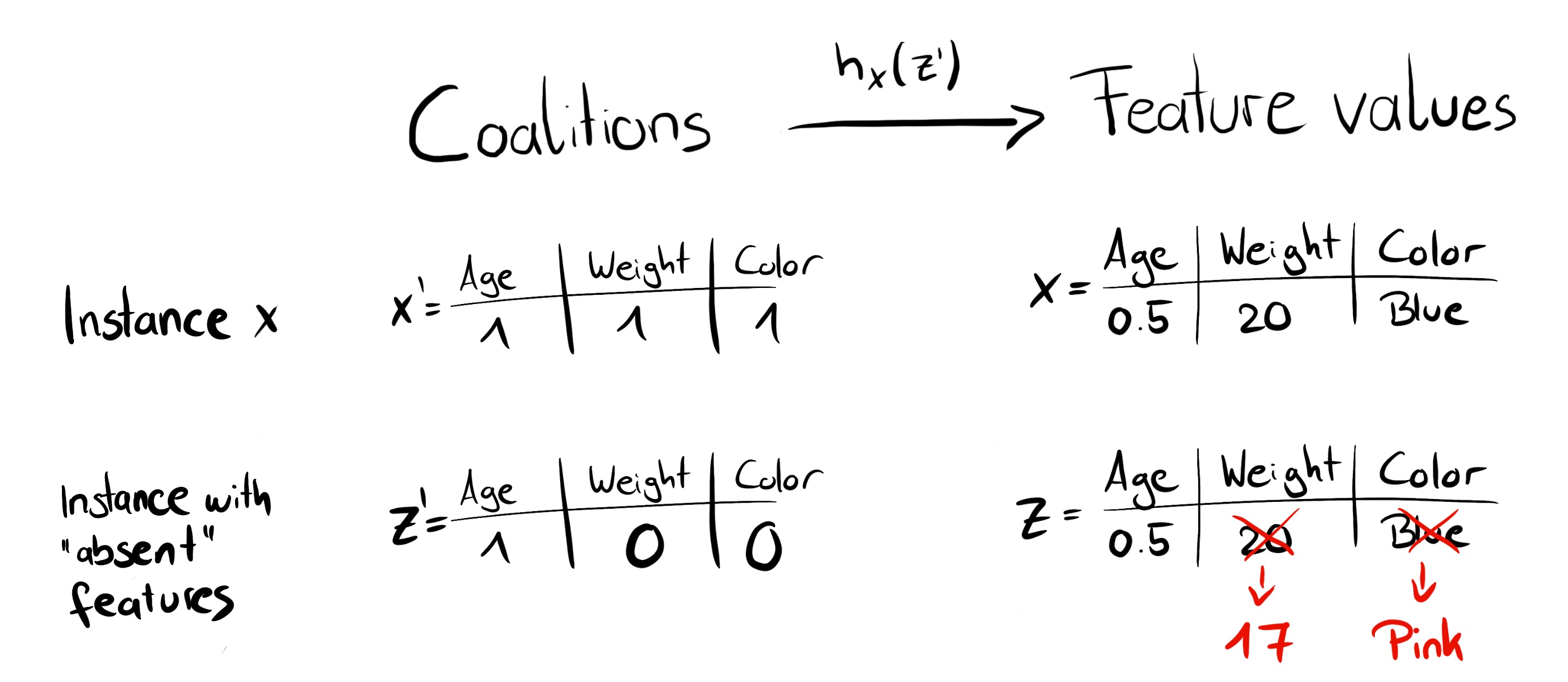
그림 5.48: h_x 함수는 연합을 유효한 인스턴스에 매핑한다. 현재 기능 (1)의 경우 h_x은 x의 형상 값에 매핑되며, 부재 기능(0)의 경우 h_x는 무작위로 샘플링된 데이터 인스턴스의 값에 매핑된다.
완벽한 세상에서 \(h_x\)는 현재 형상값을 조건으로 없는 형상값을 샘플링한다.
\[f(h_x(z')=E_{X_C|X_S}[f(x)|x_S]\]여기서 \(X_C\)는 부재 기능 집합이고 \(X_S\)는 현재 기능 집합이다. 그러나 위에서 정의한 바와 같이 표 데이터에 대한 \(h_x\)는 \(X_C\)와 \(X_S\)를 독립적으로 처리하고 한계 분포에 통합한다.
\[f(h_x(z')=E_{X_C}[f(x)]\]한계 분포에서 표본 추출은 현재 형상과 부재 형상의 의존성 구조를 무시하는 것을 의미한다. 따라서 커널SHAP는 모든 순열 기반 해석 방법과 동일한 문제를 겪는다. 그 견적은 있음직하지 않은 사례에 너무 큰 비중을 두고 있다. 결과는 믿을 수 없게 될 수 있다. 나중에 알게 되겠지만, TreeSHAP for Tree-enmble은 이 문제에 영향을 받지 않는다.
영상의 경우, 다음 그림은 가능한 매핑 기능을 설명한다.
![]()
그림 5.49: h_x 함수는 슈퍼 픽셀(sp)의 결합을 이미지에 매핑한다. 슈퍼픽셀은 픽셀 그룹이다. 현재 기능(1)의 경우 h_x는 원본 이미지의 해당 부분을 반환한다. 없는 기능(0)의 경우 h_x이(가) 해당 영역을 초과한다. 주변 픽셀의 평균 색상을 할당하는 것도 하나의 방법이 될 것이다.
LIME과의 큰 차이점은 회귀 모형의 인스턴스(instance)의 가중치 부여다. LIME은 인스턴스(instance)가 원래 인스턴스와 얼마나 가까운가에 따라 그 인스턴스(instance)를 가중시킨다. 연합 벡터에 0이 많을수록 LIME의 무게는 작아진다. SHAP는 Shapley 값 추정에서 연합군이 얻을 무게에 따라 표본 추출한 인스턴스를 가중시킨다. 작은 연탄(수치 1초)과 큰 연탄(즉, 많은 1초)은 가장 큰 가중치를 갖는다. 그 뒤의 직관은 다음과 같다. 만약 우리가 개별적인 특징에 대해 고립된 상태에서 그것의 효과를 연구할 수 있다면 우리는 가장 많은 것을 배운다. 연합이 하나의 특징으로 이루어진다면, 우리는 예측에 대한 특징들의 분리된 주요 영향에 대해 배울 수 있다. 연합이 하나의 형상을 제외한 모든 형상으로 구성된 경우, 우리는 이 형상의 총효과(주효과 + 형상 상호작용)에 대해 배울 수 있다. 연합이 특징의 절반으로 이루어진다면, 우리는 개인의 특징 기여에 대해 거의 배우지 않는데, 그 특징의 절반으로 가능한 연정이 많기 때문이다. Shapley를 준수하는 가중치를 달성하기 위해, Lundberg 등은 SHAP 커널을 제안한다.
\[\pi_{x}(z')=\frac{(M-1)}{\binom{M}{|z'|}|z'|(M-|z'|)}\]여기서 M은 최대 연합 규모와 \(|z'|\)인 경우 z’의 현재 특징의 수이다. 룬드버그와 리는 이 커널 중량에 대한 선형 회귀로 샤플리 값이 산출된다는 것을 보여준다. 연합 데이터에 LIME과 함께 SHAP 커널을 사용할 경우 LIME은 샤플리 값도 추정할 수 있다!
우리는 탄약의 샘플링에 대해 좀 더 현명해질 수 있다. 가장 작고 가장 큰 석탄이 그 무게의 대부분을 차지한다. 우리는 표본 추출 예산 K의 일부를 맹목적으로 표본 추출하는 대신에 이러한 고중량 결합을 포함시킴으로써 샤플리 가치 추정치를 더 잘 얻는다. 우리는 1과 M-1의 특징으로 가능한 모든 합금부터 시작하는데, 이것은 총 합금의 2배를 만든다. 예산이 충분히 남아 있을 때(현재 예산은 K - 2M) 2가지 특징과 M-2 기능 등을 갖춘 연합체를 포함할 수 있다. 나머지 연합 규모에서 우리는 재조정된 가중치로 샘플을 채취한다.
우리는 데이터, 목표, 가중치를 가지고 있다. 가중 선형 회귀 분석 모델을 구축하는 데 필요한 모든 사항:
\[g(z')=\phi_0+\sum_{j=1}^M\phi_jz_j'\]다음 손실 함수 L을 최적화하여 선형 모델 g를 교육한다.
\[L(f,g,\pi_{x})=\sum_{z'\in{}Z}[f(h_x(z')-g(z')]^2\pi_{x}(z')\]여기서 Z는 훈련 데이터다. 이것은 우리가 보통 선형 모형에 최적화하는 오차의 오래된 지루한 합이다. 모형의 추정 계수인 \(\phi_j\)는 샤플리 값이다.
우리는 선형 회귀 설정에 있기 때문에 회귀에 대한 표준 도구를 사용할 수도 있다. 예를 들어, 우리는 모델을 희박하게 만들기 위해 정규화 용어를 추가할 수 있다. 손실 L에 L1 페널티까지 더하면 희박한 설명을 만들 수 있다. (결과 계수가 여전히 유효한 샤플리 값인지 확실하지 않음)
TreeSHAP
룬드버그 외 연구진(2018)2은 의사결정 나무, 랜덤 숲, 그라데이션 상승 나무와 같은 트리 기반 기계 학습 모델을 위한 SHAP의 변형 모델인 TreeSHAP를 제안했다. TreeSHAP는 빠르고, 정확한 Shapley 값을 계산하며, 형상이 종속된 경우 Shapley 값을 정확하게 추정한다. 이에 비해 커널SHAP는 계산에 비용이 많이 들고 실제 샤플리 값에 근사할 뿐이다.
TreeSHAP는 얼마나 빠른가? 정확한 샤플리 값의 경우, 연산 복잡도를 \(O(TL2^M)\)에서 \(O(TLD^2)\)로, 여기서 T는 나무의 수이며, L은 모든 나무의 최대 잎 수이며 D는 나무의 최대 깊이이다.
TreeSHAP는 올바른 조건부 기대치 \(E_{X_S|X_C}(f(x)|x_S)\)를 추정한다. 단일 트리, 인스턴스 x 및 형상 부분집합 S에 대한 예상 예측을 계산하는 방법에 대해 직관적으로 설명하겠다. 만일 S가 모든 형상의 집합이라면, 모든 형상의 집합이라면, 인스턴스 x가 떨어지는 노드의 예측은 예상된 예측이 될 것이다. S가 비어 있는 경우, 어떤 형상에 대해서도 조건을 제시하지 않으면 모든 단자 노드의 예측 가중 평균을 사용할 것이다. S에 일부 기능이 있지만 전부는 아닌 경우, 우리는 연결할 수 없는 노드의 예측을 무시한다. 연결할 수 없다는 것은 이 노드로 이어지는 의사결정 경로가 \(x_S\)의 값과 모순된다는 것을 의미한다. 나머지 단자 노드에서 노드 크기에 따라 가중치가 부여된 예측(즉, 해당 노드의 교육 샘플 수)을 평균한다. 노드당 인스턴스 수로 가중되는 나머지 터미널 노드의 평균은 주어진 S에 대한 예상 예측이다. 문제는 형상값의 가능한 각 부분집합 S에 대해 이 절차를 적용해야 한다는 것이다. 다행히 TreeSHAP는 지수 대신 다항식 시간으로 계산한다. 기본적인 생각은 가능한 모든 잠수정 S를 동시에 나무 아래로 밀어 넣는 것이다. 각 결정 노드에 대해 우리는 하위 집합의 수를 추적해야 한다. 이는 상위 노드의 하위 집합과 분할 피쳐에 따라 달라진다. 예를 들어 트리의 첫 번째 분할이 형상 x3에 있을 때 형상 x3을 포함하는 모든 하위 집합이 하나의 노드(x가 가는 노드)로 이동한다. 기능 x3이 포함되지 않은 서브셋은 무게가 줄어든 두 노드로 이동한다. 불행히도, 크기가 다른 서브셋들은 다른 무게를 가지고 있다. 알고리즘은 각 노드에서 서브셋의 전체 중량을 추적해야 한다. 이것은 알고리즘을 복잡하게 만든다. TreeSHAP에 대한 자세한 내용은 원본 문서를 참조하십시오. 연산은 더 많은 나무로 확장될 수 있다. 샤플리 값의 부가성 특성 덕분에 나무 앙상블의 샤플리 값은 개별 트리의 샤플리 값의 (가중치) 평균이다.
다음으로, 우리는 실제의 SHAP 설명을 살펴볼 것이다.
예시
나는 [경추암에 대한 위험]을 예측하기 위해 100그루의 나무로 무작위 삼림 분류기를 훈련시켰다. 우리는 개별적인 예측을 설명하기 위해 SHAP를 사용할 것이다. 임의의 숲은 나무의 앙상블이기 때문에 느린 커널SHAP 방법 대신 빠른 TreeSHAP 추정 방법을 사용할 수 있다.
SHAP는 Shapley 값을 계산하므로, 해석은 Shapley 값 장과 동일하다. 그러나 Python Shapp 패키지는 다른 시각화를 제공한다. Shapley 값과 같은 피쳐 속성을 “forces”로 시각화할 수 있다. 각 형상 값은 예측을 증가시키거나 감소시키는 힘이다. 예측은 기준선부터 시작한다. 샤플리 값의 기준선은 모든 예측의 평균이다. 그림에서 각 샤플리 값은 예측을 증가(양수 값)하거나 감소(음수 값)하도록 밀어주는 화살표다. 이러한 힘은 데이터 인스턴스의 실제 예측에서 서로 균형을 맞춘다.
다음 그림은 자궁경부암 데이터 집합에서 두 명의 여성을 위한 SHAP 설명 힘 그림을 보여준다.

그림 5.50: SHAP 값은 두 개인의 예측된 암 확률을 설명한다. 평균 예측 확률인 기준선은 0.066이다. 첫 번째 여성은 0.06의 낮은 예측 위험을 가지고 있다. 성병 등 위험증가 효과는 연령 등의 영향을 줄임으로써 상쇄된다. 두 번째 여성은 0.71의 높은 위험성을 가지고 있다. 51세, 34세 흡연으로 인해 그녀는 암에 걸릴 것으로 예상했다.
이것은 개별적인 예측에 대한 설명이었다.
샤플리 값은 글로벌 설명으로 결합될 수 있다. 모든 인스턴스에 대해 SHAP를 실행하면 Shapley 값의 행렬이 나타난다. 이 매트릭스는 데이터 인스턴스당 하나의 행과 형상당 하나의 열을 가지고 있다. 이 행렬의 샤플리 값을 분석하여 전체 모델을 해석할 수 있다.
우리는 SHAP 기능의 중요성으로 시작한다.
SHAP Feature Importance
SHAP 기능의 중요성에 대한 아이디어는 간단하다. 절대 샤플리 값이 큰 특징이 중요하다. 글로벌 중요성을 원하기 때문에 전체 데이터에서 형상당 절대 샤플리 값을 평균화한다.
\[I_j=\sum_{i=1}^n{}|\phi_j^{(i)}|\]다음으로, 우리는 중요성을 감소시킴으로써 특징들을 분류하고 그것들을 구성한다. 다음 그림은 자궁경부암 예측을 위해 훈련된 임의의 숲에 대한 SHAP 기능의 중요성을 보여준다.
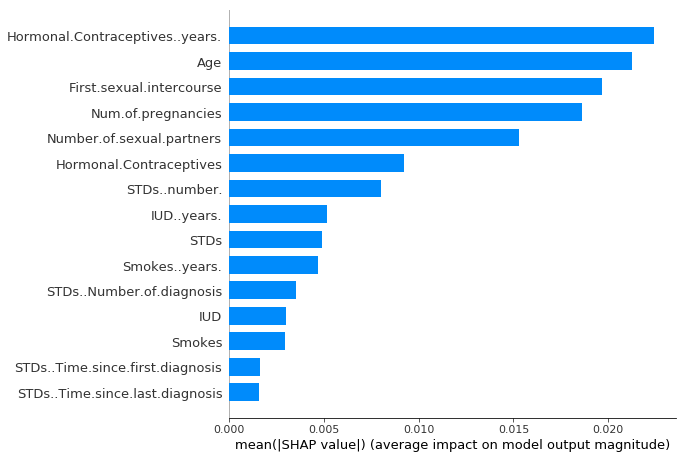
그림 5.51: SHAP 피쳐 중요도는 평균 절대 샤플리 값으로 측정된다. 호르몬 피임약을 사용한 연수가 가장 중요한 특징으로, 예측된 절대암 발생 확률을 평균 2.4%포인트(X축에 0.024)로 변경했다.
SHAP 특성 중요성은 정자 특성 중요도의 대안이다. 두 가지 중요도 조치 사이에는 큰 차이가 있다. 퍼머테이션 특성의 중요성은 모델 성능의 감소에 기초한다. SHAP는 형상 속성의 크기에 기초한다.
형상 중요도 그림은 유용하지만, 가져오기 이상의 정보는 포함하지 않는다. 좀 더 유용한 플롯을 위해, 우리는 다음 요약 플롯을 살펴볼 것이다.
SHAP Summary Plot
요약 그림은 형상 중요도와 형상 효과를 결합한다. 요약 그림의 각 점은 형상과 인스턴스에 대한 Shapley 값이다. Y축의 위치는 형상에 의해, X축은 샤플리 값에 의해 결정된다. 색상은 낮은 값에서 높은 값까지 형상의 값을 나타낸다. 겹치는 점은 y축 방향으로 산란되므로 형상당 샤플리 값의 분포를 알 수 있다. 그 특징들은 중요도에 따라 배열되어 있다.
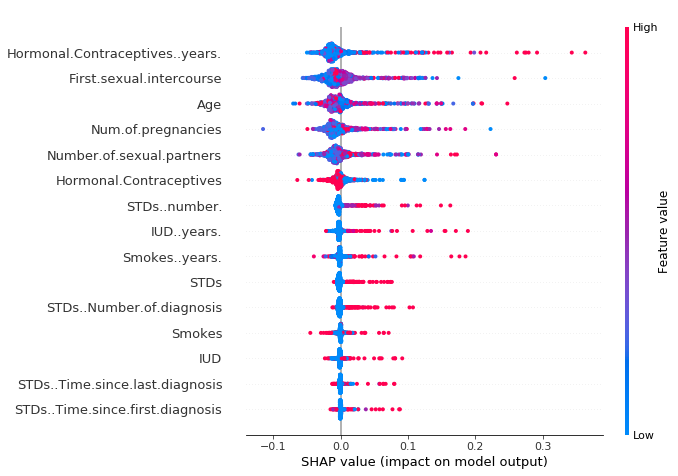
그림 5.52: SHAP 요약 그림. 호르몬 피임약을 복용하는 기간이 적을수록 암의 위험이 감소하고, 많은 해가 되면 그 위험이 증가한다. 정기적인 알림: 모든 효과는 모델의 행동을 묘사하며 현실 세계에서 반드시 인과관계가 있는 것은 아니다.
요약 그림에서는 형상의 값과 예측에 미치는 영향 사이의 관계를 나타내는 첫 번째 징후를 본다. 그러나 정확한 관계 형태를 보려면 SHAP 의존도를 살펴봐야 한다.
SHAP Dependence Plot
SHAP 피쳐 의존성은 가장 단순한 전역 해석 그림일 수 있다. 1) 형상을 고른다. 2) 각 데이터 인스턴스에 대해 x축에 형상값과 y축에 해당하는 샤플리 값으로 점을 표시한다. 3) 끝났어
수학적으로 플롯에는 \(\{(x_j^{(i)},\phi_j^{(i)}\}_{i=1}^n\)이 들어 있다.
다음 그림은 수년간 호르몬 피임제에 대한 SHAP 기능 의존성을 보여준다.
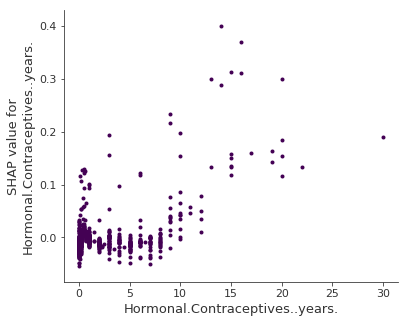
그림 5.53: 호르몬 피임약들에 대한 SHAP 의존도. 0년에 비해 몇 년은 예측 확률을 낮추고 높은 햇수는 예측된 암 확률을 높인다.
SHAP 의존도 그림은 부분 의존도 그림과 누적 국소 효과의 대안이다. PDP와 ALE 플롯은 평균 효과를 나타내지만, SHAP 의존성은 y축에 대한 분산을 보여준다. 특히 상호작용의 경우, SHAP 의존도도는 Y축에 훨씬 더 분산된다. 이러한 형상 교호작용을 강조함으로써 의존도 그림을 개선할 수 있다.
SHAP Interaction Values
상호작용 효과는 개별 형상 효과를 고려한 후 추가 결합 형상 효과다. 게임 이론의 샤플리 상호작용 지수는 다음과 같이 정의된다.
\[\phi_{i,j}=\sum_{S\subseteq\setminus\{i,j\}}\frac{|S|!(M-|S|-2)!}{2(M-1)!}\delta_{ij}(S)\]\(i\neq{}j\)일 때 및:
\[\delta_{ij}(S)=f_x(S\cup\{i,j\})-f_x(S\cup\{i\})-f_x(S\cup\{j\})+f_x(S)\]이 공식은 형상의 주효과를 빼서 개별적인 효과를 고려한 후에 순수한 상호작용 효과를 얻도록 한다. 우리는 샤플리 값 계산에서와 같이 가능한 모든 형상 연고 S의 값을 평균한다. 모든 형상에 대해 SHAP 상호 작용 값을 계산할 때, 우리는 M x M 치수를 가진 인스턴스당 하나의 매트릭스를 얻는데, 여기서 M은 형상의 수입니다.
어떻게 상호작용 지수를 사용할 수 있을까? 예를 들어, SHAP 피쳐 의존도를 가장 강한 상호 작용으로 자동으로 색칠하려면:
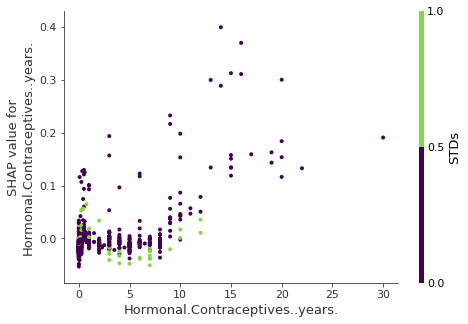
그림 5.54: SHAP 피쳐 의존도와 상호작용 시각화. 호르몬 피임약의 해는 성병과 상호작용을 한다. 0년에 가까운 경우, 성병의 발생은 예측된 암 위험을 증가시킨다. 피임약에서 더 많은 해 동안, 성병의 발생은 예측된 위험을 감소시킨다. 다시 말하지만, 이것은 인과 모델이 아니다. 효과는 교란 요인에 기인할 수 있다(예: 성병과 낮은 암 위험은 더 많은 의사 방문과 상관관계가 있을 수 있다).
Clustering SHAP values
Shapley 값을 사용하여 데이터를 클러스터링할 수 있다. 클러스터링의 목표는 유사한 인스턴스 그룹을 찾는 것이다. 일반적으로 클러스터링은 형상에 기초한다. 특징들은 종종 다른 척도에 있다. 예를 들어, 높이는 미터 단위로 측정되고, 색도는 0 ~ 100이며, 센서 출력은 -1과 1 사이일 수 있다. 어려운 점은 이렇게 서로 다른 비비교적 기능을 가진 인스턴스 간의 거리를 계산하는 것이다.
SHAP 클러스터링은 각 인스턴스의 Shapley 값에 따라 클러스터링하여 작동한다. 이는 유사성에 대한 설명으로 인스턴스를 클러스터링한다는 것을 의미한다. 모든 SHAP 값은 예측 공간의 단위인 동일한 단위를 갖는다. 어떤 클러스터링 방법이라도 사용할 수 있다. 다음 예제에서는 계층적 집합적 클러스터링을 사용하여 인스턴스 순서를 정한다.
플롯은 많은 힘 그림으로 이루어져 있으며, 각각의 그림들은 한 예시의 예측을 설명한다. 힘 그림을 수직으로 회전시켜 군집화 유사성에 따라 나란히 배치한다.
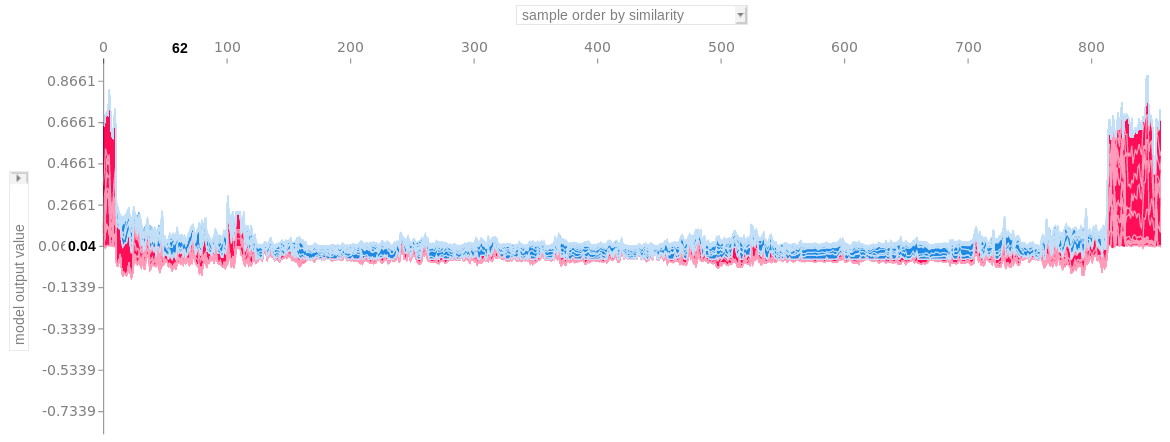
그림 5.55: 스택형 SHAP 설명(설명 유사성)으로 클러스터링됨 x축의 각 위치는 데이터의 인스턴스(instance)이다. 빨간색 SHAP 값은 예측을 증가시키고, 파란색 값은 예측을 감소시킨다. 성단이 눈에 띈다: 오른쪽에는 암 발병률이 높은 그룹이 있다.
장점
SHAP는 Shapley 값을 계산하므로 Shapley 값의 모든 장점이 적용된다. SHAP는 게임 이론에서 *의 확고한 이론적 토대를 가지고 있다. 예측치는 형상값 중 **공정한 분포이다. 우리는 예측과 평균 예측을 비교하는 **대조적인 설명을 받는다.
SHAP LIME 및 Shapley 값 연결 이것은 두 가지 방법을 더 잘 이해하는데 매우 유용하다. 해석 가능한 기계학습 분야를 통일하는 데도 도움이 된다.
SHAP는 트리 기반 모델에 대해 빠른 구현을 가지고 있다. 나는 이것이 SHAP의 인기의 열쇠라고 믿는다. 왜냐하면 Shapley 값의 채택을 위한 가장 큰 장벽은 느린 계산이기 때문이다.
빠른 연산 덕분에 글로벌 모델 해석에 필요한 많은 샤플리 값을 계산할 수 있다. 전역 해석 방법에는 형상 중요도, 형상 의존도, 상호작용, 군집화 및 요약 그림이 포함된다. SHAP의 경우 샤플리 값은 글로벌 해석의 “원자 단위”이기 때문에 글로벌 해석은 현지 설명과 일치한다. LIME을 국소적 설명과 부분 의존도 그림 및 글로벌 설명에 중요한 특징에 사용할 경우 공통의 기반이 부족하다.
단점
KernelSHAP는 느리다. 따라서 많은 인스턴스에 대한 샤플리 값을 계산하고 싶을 때 커널SHAP를 사용할 수 없게 된다. 또한 SHAP 기능 중요도와 같은 모든 글로벌 SHAP 방법은 많은 인스턴스에 대해 샤플리 값을 계산해야 한다.
KernelSHAP는 피쳐 의존성을 무시한다. 대부분의 다른 순열 기반 해석 방법에는 이러한 문제가 있다. 형상 값을 임의 인스턴스(instance)의 값으로 대체함으로써, 일반적으로 한계 분포에서 무작위로 샘플링하는 것이 더 쉽다. 그러나, 예를 들어 상관관계가 있는 형상에 따라 달라지는 경우, 이는 예상할 수 없는 데이터 점에 너무 많은 비중을 두게 된다. TreeSHAP는 조건부 예상 예측을 명시적으로 모델링하여 이 문제를 해결한다.
샤플리 값의 단점은 SHAP에도 적용된다. Shappley 값은 잘못 해석될 수 있으며, TreeSHAP를 제외하고 새로운 데이터를 계산하기 위해 데이터에 대한 액세스가 필요하다.
소프트웨어
저자들은 shap Python 패키지에서 SHAP를 구현했다. 이 구현은 Scikit-Learn for Python)의 트리 기반 모델에 적용된다. 이 챕터의 예시에도 잽 패키지가 사용되었다. SHAP는 트리 부스팅 프레임워크 xgboost와 LightGBM에 통합되어 있다. R에는 shapper 패키지가 있다. SHAP는 R xgboost 패키지에 포함되어 있다.
-
Lundberg, Scott M., and Su-In Lee. “A unified approach to interpreting model predictions.” Advances in Neural Information Processing Systems. 2017. ↩
-
Lundberg, Scott M., Gabriel G. Erion, and Su-In Lee. “Consistent individualized feature attribution for tree ensembles.” arXiv preprint arXiv:1802.03888 (2018). ↩