5.4 Feature Interaction
Feature Interaction
특성이 예측 모델에서 상호 작용하는 경우 한 특성의 효과가 다른 특성의 값에 따라 다르기 때문에 예측을 특성 효과의 합으로 표시할 수 없습니다. 아리스토텔레스의 말한 “전체가 부분의 합보다 크다”는 상호작용이 있는 곳에 적용됩니다.
특성 상호작용이란?
머신러닝 모델이 두 가지 특성을 기반으로 예측하는 경우 예측을 네 가지 항으로 분해할 수 있습니다. 상수 항, 첫 번째 특성에 대한 항, 두 번째 특성에 대한 항 및 두 특성의 상호작용을 나타내는 항입니다. 두 특성 간의 상호 작용은 개별 특성 효과를 고려한 후 특성을 변경하여 발생하는 예측의 변화입니다.
예를 들어 모델은 주택 크기(크거나 작음)와 위치(좋거나 나쁘거나)를 특성로 사용하여 주택의 가치를 예측합니다. 이 경우 다음과 같은 네 가지 예측이 가능합니다.
| Location | Size | Prediction |
|---|---|---|
| good | big | 300,000 |
| good | small | 200,000 |
| bad | big | 250,000 |
| bad | small | 150,000 |
모델 예측을 다음 부분으로 분해합니다. 상수 항(150,000), 크기 특성(크면 +100,000 작으면 +0) 및 위치(좋으면 +50,000 나쁘면 +0)에 대한 효과입니다. 이 분해는 모델 예측을 완벽하게 설명합니다. 모델 예측은 크기 및 위치에 대한 단일 특성 효과를 합한 것이기 때문에 상호 작용 효과는 없습니다. 작은 집을 크게 만들면, 위치와 상관없이 예측은 항상 100.000씩 증가합니다. 또한, 좋은 위치와 나쁜 위치의 예측 차이는 크기에 상관없이 50,000입니다.
이제 상호 작용이 있는 예를 살펴보겠습니다.
| Location | Size | Prediction |
|---|---|---|
| good | big | 400,000 |
| good | small | 200,000 |
| bad | big | 250,000 |
| bad | small | 150,000 |
예측 표를 다음 부분으로 분해합니다. 상수 항(150,000), 크기 특성(크면 +100,000, 작으면 +0) 및 위치(좋으면 +50,000, 나쁘면 +0)에 대한 효과입니다. 이 표의 경우, 상호작용을 위한 추가 항이 필요합니다. 집이 크고 좋은 위치에 있다면 +100,000 입니다. 이것은 크기와 위치의 상호작용입니다. 이 경우 큰 집과 작은 집의 예측 차이는 위치에 따라 다르기 때문입니다.
교호작용 강도를 추정하는 한 가지 방법은 특성의 교호작용에 따라 예측 변동의 양을 측정하는 것입니다. 이러한 측정은 Friedman and Popescu(2008)1에 의해 소개된 H-statistic이라고 합니다.
이론: Friedman’s H-statistic
우리는 두 가지 경우를 다루려고 합니다. 첫째, 모델의 두 특성이 서로 상호 작용하는지 여부를 알려 주는 양방향 상호 작용 측정입니다. 둘째, 모델의 특성이 다른 모든 특성와 상호 작용하는지 여부를 알려 주는 총 상호 작용 측정입니다. 이론적으로, 임의의 수의 특성들 사이의 임의적인 상호작용을 측정할 수 있지만, 이 두 가지가 가장 흥미로운 경우입니다.
두 가지 특성이 상호 작용하지 않는 경우, 다음과 같이 부분 의존성 특성을 분해할 수 있습니다(부분 의존성 함수가 0으로 중심에 있다고 가정).
\[PD_{jk}(x_j,x_k)=PD_j(x_j)+PD_k(x_k)\]여기서 \(PD_{jk}(x_j,x_k)\)는 두 특성의 양방향 부분 의존 함수이며 \(PD_j(x_j)\) 및 \(PD_k(x_k)\) 단일 특성의 부분 의존 함수입니다.
마찬가지로, 특성이 다른 특성과 상호 작용하지 않는 경우, 예측 함수 \(\hat{f}(x)\)을 부분 의존 함수의 합으로 표현할 수 있습니다. 여기서 첫 번째 합계는 j에, 두 번째 합은 j를 제외한 다른 모든 특성에 따라 달라집니다.
\[\hat{f}(x)=PD_j(x_j)+PD_{-j}(x_{-j})\]여기서 \(PD_{-j}(x_{-j})\)는 j-th 특성을 제외한 모든 특성에 종속되는 부분 의존 함수입니다.
이 분해는 상호 작용 없는 부분 의존성(또는 전체 예측) 함수를 나타냅니다(각각 특성 j와 k 간 또는 각각 j와 다른 모든 특성 간). 다음 단계에서는 관찰된 부분 의존성 함수와 상호 작용 없는 분해된 함수의 차이를 측정합니다. 부분 의존도(두 특성 간의 상호 작용을 측정하기 위해) 또는 전체 함수(특성와 다른 모든 특성 간의 상호 작용을 측정하기 위해) 출력의 분산을 계산합니다. 교호작용에 의해 설명된 분산량(관측된 PD와 상호 작용이 없는 PD 간의 차이)은 교호작용 강도 통계량으로 사용됩니다. 통계는 상호 작용이 전혀 없는 경우 0이고 \(PD_{jk}\) 또는 \(\hat{f}\)의 모든 분산을 부분 의존성 함수의 합으로 설명하는 경우 1입니다. 두 특성 사이의 교호작용 통계가 1이면 각 단일 PD 함수가 일정하며 예측에 미치는 영향은 교호작용만 통해 온다는 것을 의미합니다. H-statistic는 1보다 클 수도 있으므로 이 경우는 해석하기가 더 어렵습니다. 이 문제는 2차원 부분 의존도 그림의 분산보다 양방향 교호작용의 분산이 더 큰 경우에 발생할 수 있습니다.
수학적으로 특성 j와 k의 상호작용을 위해 Friedman과 Popescu가 제안한 H-statistic은 다음과 같습니다.
\[H^2_{jk}=\sum_{i=1}^n\left[PD_{jk}(x_{j}^{(i)},x_k^{(i)})-PD_j(x_j^{(i)})-PD_k(x_{k}^{(i)})\right]^2/\sum_{i=1}^n{PD}^2_{jk}(x_j^{(i)},x_k^{(i)})\]특성 j가 다른 특성과 상호 작용하는지 여부를 측정하는 경우에도 마찬가지입니다.
\[H^2_{j}=\sum_{i=1}^n\left[\hat{f}(x^{(i)})-PD_j(x_j^{(i)})-PD_{-j}(x_{-j}^{(i)})\right]^2/\sum_{i=1}^n\hat{f}^2(x^{(i)})\]H-statistic 분석은 모든 데이터 지점에 반복되므로 평가 비용이 많이 듭니다. 각 시점마다 부분 의존성을 평가해야 하며, 이는 모든 n개의 데이터 지점에서 수행됩니다. 최악의 경우, 머신러닝 모델에 대한 양방향 H-statistic(j vs. k)을 계산하기 위한 \(2n^2\) 및 총 H-statistic(j-vs. all)에 대한 \(3n^2\)를 호출해야 합니다. 계산 속도를 높이기 위해 n개 데이터 지점에서 샘플을 추출할 수 있습니다. 이는 부분 의존성 추정치의 분산을 증가시켜 H-statistic 불안정을 유발하는 단점이 있습니다. 따라서 샘플링을 사용하여 계산 부담을 줄이는 경우 데이터 지점을 충분히 샘플링해야 합니다.
또한 Friedman 및 Popescu는 H-statistic이 0과 유의하게 다른지 여부를 평가하기 위한 테스트 통계를 제안합니다. 귀무 가설은 교호작용이 없다 입니다. 귀무 가설에서 교호작용 통계를 생성하려면 특성 j와 k 또는 다른 모든 것 간의 교호작용이 없도록 모델을 조정할 수 있어야 합니다. 일부 모델 유형에서는 이 작업을 수행할 수 없습니다. 따라서 이 테스트는 model-specific이고 model-agnostic이 아닙니다. 여기에 대해서는 더이상 다루지 않습니다.
예측이 확률인 경우 교호작용 강도 통계량을 분류 문제에도 적용할 수 있습니다.
예시
실제 특성 상호 작용이 어떤 모습인지 확인해 보겠습니다! 날씨 및 캘린더 특성을 기반으로 자전거 대여의 수를 예측하는 서포트 벡터 머신에서 특성의 상호작용 강도를 측정합니다. 다음 그림은 특성 교호작용 H-statistic 특성을 보여 줍니다.

그림 5.24: 자전거 대여를 예측하는 서포트 벡터 머신의 다른 모든 특성과 각 특성에 대한 상호 작용 강도(H-statistic)입니다. 전반적으로 특성 간의 상호 작용 효과는 매우 약합니다(특성당 설명된 10% 미만의 분산).
다음 예에서는 분류 문제에 대한 상호 작용 통계를 계산합니다. 일부 위험 요인을 감안하여, 랜덤 포레트스의 특징들 간의 상호작용을 분석합니다.
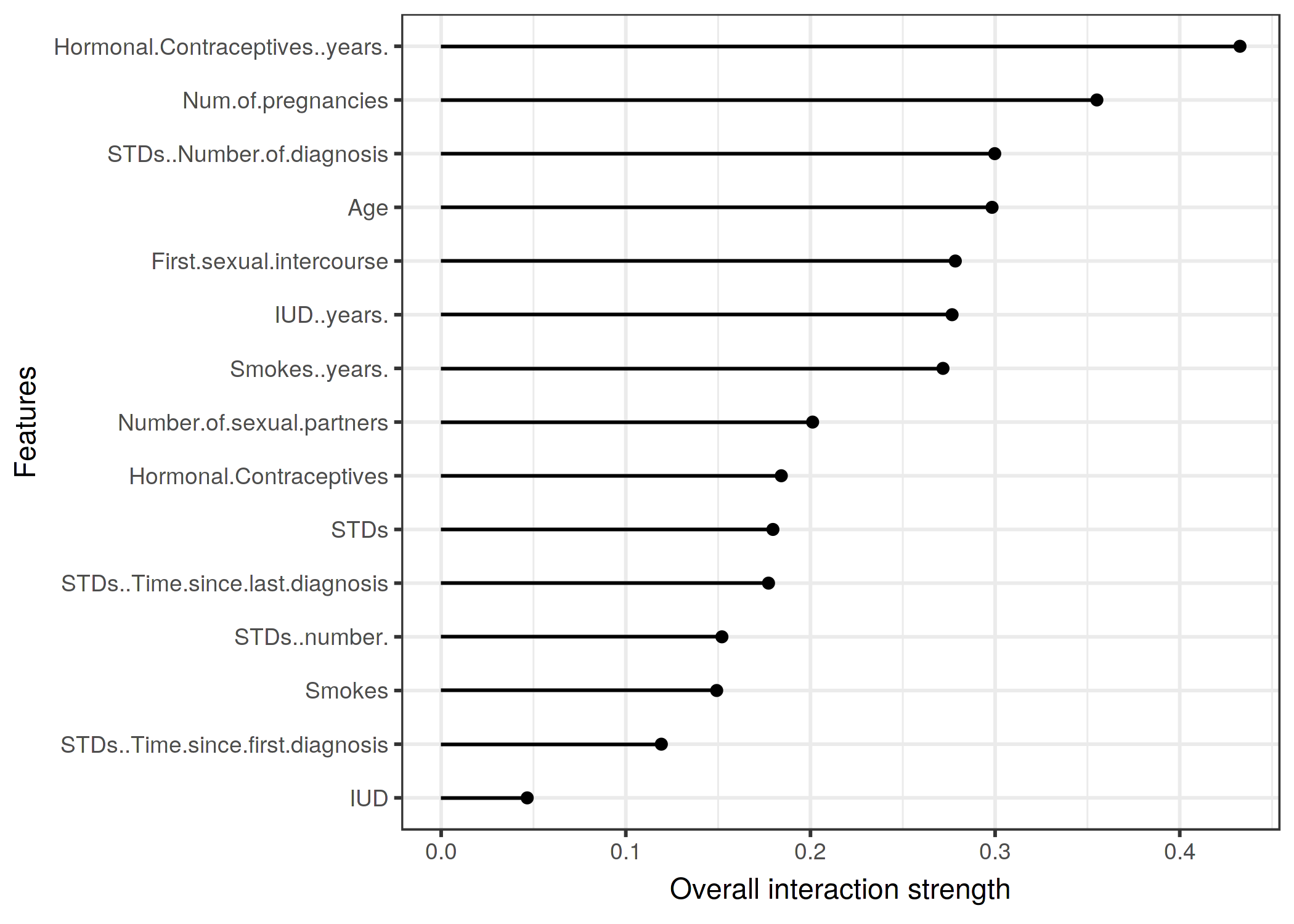
그림 5.25: 각 특성에 대한 상호작용 강도(H-statistic)는 자궁경부암의 확률을 예측하는 랜덤 포리스트에 대한 다른 모든 특성과 동일합니다. 호르몬 피임약의 복용 연수는 다른 모든 특징들과 가장 높은 상대적 상호작용 효과를 가지고 있고, 이어서 임신 횟수가 있습니다.
다른 모든 특성와 각 특성의 특성 상호 작용을 확인한 후 특성 중 하나를 선택하고 선택한 특성와 다른 특성 간의 모든 양방향 상호 작용을 자세히 살펴볼 수 있습니다.
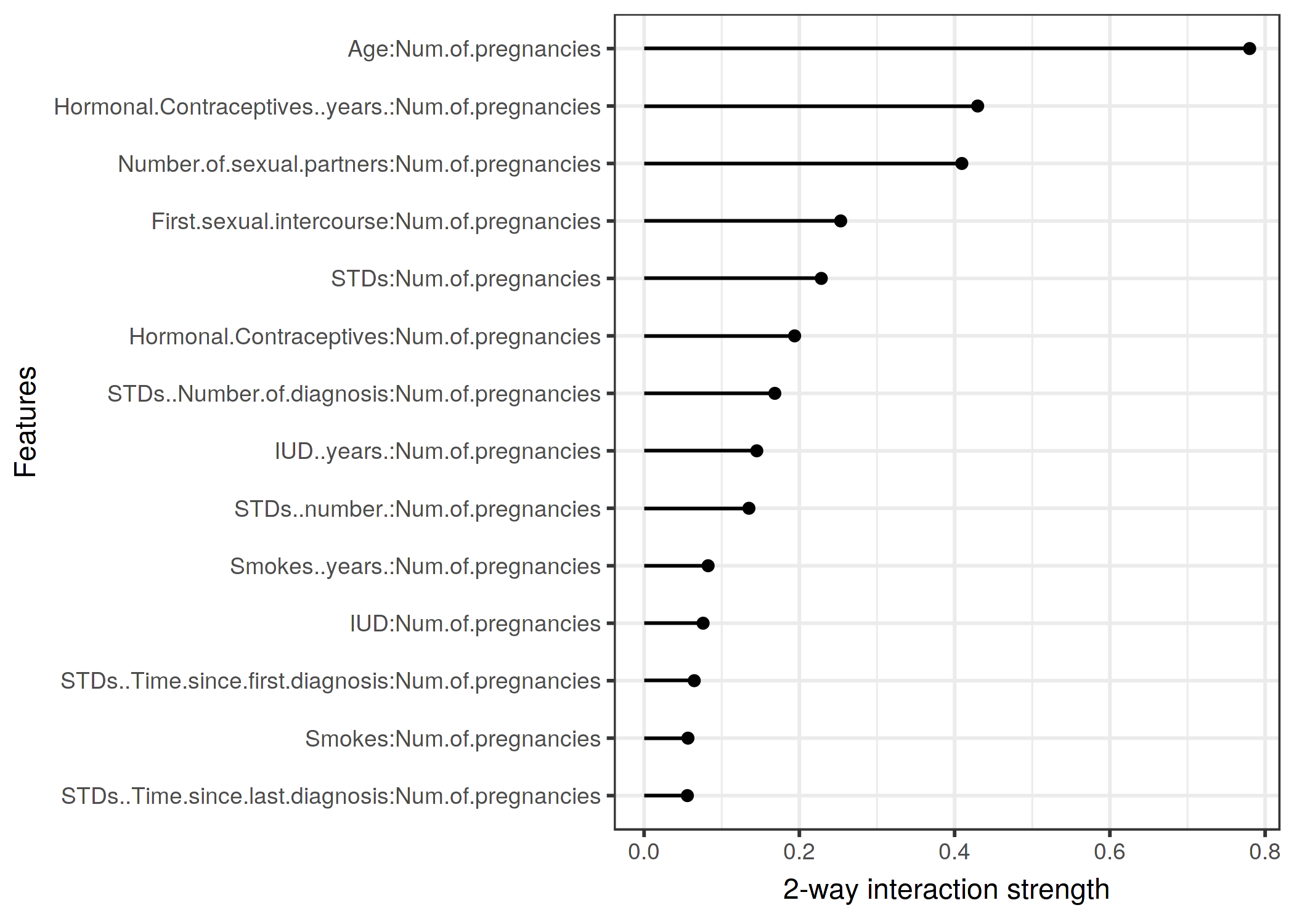
그림 5.26: 임신 횟수와 서로 다른 특징 사이의 양방향 상호작용 강도(H-statistic)입니다. 임신 횟수와 나이 사이에는 강한 상호작용이 있습니다.
장점
H-statistic 상호작용에는 부분 의존성 분해를 기반으로하는 이론이 있습니다.
H-statistic은 의미있는 해석을 가집니다. 교호작용은 교호작용에 의해 설명되는 분산 공유로 정의됩니다.
이 통계는 차원과 관계가 없기 때문에 특성 및 모델 간에 비교할 수 있습니다.
통계 특정 형식에 관계없이 모든 종류의 상호 작용을 탐지합니다.
H-statistic을 사용하면 3개 이상의 특성 간의 상호 작용 강도 같은 임의 높은 상호 작용을 분석할 수도 있습니다.
단점
가장 먼저 알게 될 사항은 다음과 같습니다. H-statistic 상호작용은 계산 비용이 비싸기 때문에 계산하는 데 오랜 시간이 걸립니다.
계산에는 한계 분포를 추정하는 작업이 포함됩니다. 또한 이러한 추정에는 데이터 점을 모두 사용하지 않는 경우의 특정 분산이 있습니다. 즉, 점을 샘플링하면 실행마다 추정치가 다르며 결과가 불안정할 수 있습니다. 안정적인 결과를 얻을 수 있는 데이터가 충분한지 확인하기 위해 H-statistic연산을 몇 번 반복하는 것이 좋습니다.
교호작용이 0보다 유의하게 큰지 여부는 불분명합니다. 통계 테스트를 수행해야 하지만 이 테스트는 model-agnostic 버전에서 (아직) 사용할 수 없습니다.
평가 문제와 관련하여, H-statistic이 우리가 “강한”의 상호작용을 고려할 수 있을 만큼 충분히 큰지를 말하는 것은 어렵습니다.
또한 H-statistic은 1보다 클 수 있어 해석이 어렵습니다.
H-statistic은 우리에게 상호작용의 강도를 알려 주지만, 상호작용이 어떻게 보이는지는 알려주지 않습니다. 그것이 부분 의존도의 목적입니다. 의미 있는 순서는 상호 작용 강도를 측정한 다음 관심 있는 교호작용에 대한 2D 부분 의존도 그림을 만드는 것입니다.
입력이 픽셀인 경우 H-statistic을 의미 있게 사용할 수 없습니다. 따라서 이 기술은 이미지 분류에 유용하지 않습니다.
상호 작용 통계는 특성를 독립적으로 섞을 수 있다는 가정 하에 작동합니다. 특성이 강하게 상관관계가 있는 경우, 가정은 위반되며 우리는 현실에서 매우 가능성이 없는 특성 조합을 통합합니다. 그것은 부분 의존도 그림과 같은 문제입니다. 그것이 과대평가나 과소평가로 이어진다면 일반화했다고 말할 수 없습니다.
때로는 결과가 이상하고 소규모 시뮬레이션의 경우 기대된 결과를 산출하지 않습니다. 하지만 이것은 개인적인 경험입니다.
구현
이 책의 예시는 CRAN, Github에서 이용할 수 있는 R 패키지 iml을 사용하였습니다.
특정 모델에 중점을 둔 다른 구현도 있습니다.
R 패키지 pre는 RuleFit 및 H-statistic을 구현합니다.
R 패키지 gbm는 경사 부스팅 모델과 H-statistic 모델을 구현합니다.
대안책
H-statistic은 상호 작용을 측정하는 유일한 방법이 아닙니다.
Hooker(2004)2의 VIN(Variable Interaction Networks)은 예측 함수를 주효과 및 특성 교호작용으로 분해하는 접근법입니다. 그러면 특성 간의 상호 작용이 네트워크로 시각화됩니다. 유감스럽게도 아직 소프트웨어를 사용할 수 없습니다.
Greenwell 등(2018)3의 부분 의존성 기반 특성 상호 작용은 두 특성 간의 상호 작용을 측정합니다. 이 접근방식은 다른 특성의 서로 다른 고정점을 조건으로 한 특성의 특성 중요도(부분 의존성 함수의 분산으로 정의됨)를 측정합니다. 분산이 높은 경우 특성은 서로 상호 작용하고 0이면 상호 작용하지 않습니다. 해당 R 패키지 vip는 Github에서 사용할 수 있습니다. 또한 이 패키지는 부분 의존도 그림 및 특성 중요도를 다룹니다.
-
Friedman, Jerome H, and Bogdan E Popescu. “Predictive learning via rule ensembles.” The Annals of Applied Statistics. JSTOR, 916–54. (2008). ↩
-
Hooker, Giles. “Discovering additive structure in black box functions.” Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining. (2004). ↩
-
Greenwell, Brandon M., Bradley C. Boehmke, and Andrew J. McCarthy. “A simple and effective model-based variable importance measure.” arXiv preprint arXiv:1805.04755 (2018). ↩