6.1 Counterfactual Explanations
Counterfactual Explanations
반사실적 설명은 “X가 발생하지 않았다면 Y가 발생하지 않았을 것”이라는 형태로 인과관계를 설명합니다. 예를 들어, “내가 이 뜨거운 커피를 한 모금 마시지 않았다면, 나는 혀를 태우지 않았을 거예요. 이벤트 Y는 제가 혀를 데었다는 것입니다. 왜냐하면 X는 뜨거운 커피를 마셨기 때문입니다. 반사실적 사고를 하는 것은 관찰된 사실들과 모순되는 가상의 현실을 상상하는 것을 요구합니다(예: 뜨거운 커피를 마시지 않은 세계). 따라서 “반사실적”이라는 이름이 필요합니다. 반사실적인 사고 능력은 우리 인간들을 다른 동물들에 비해 매우 똑똑하게 만듭니다.
해석 가능한 기계 학습에서는 개별 인스턴스의 예측을 설명하기 위해 반사실적 설명을 사용할 수 있습니다. “이벤트”는 인스턴스의 예측된 결과이며, “원인”은 모형에 입력되고 특정 예측을 “발생”한 이 인스턴스의 특정 형상 값입니다. 그래프로 표시되며 입력과 예측 간의 관계는 매우 간단합니다. 피쳐 값이 예측의 원인입니다.
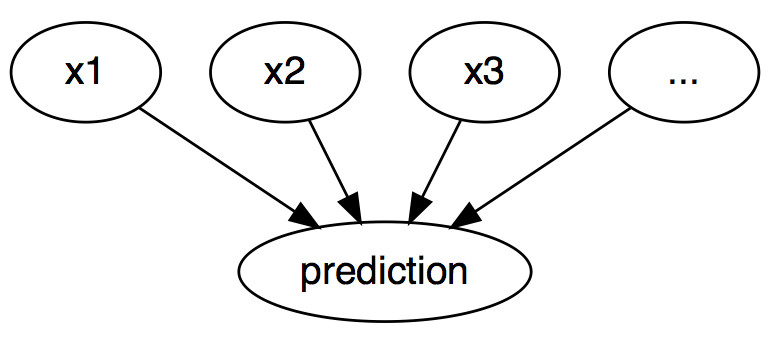
그림 6.1: 기계 학습 모델의 입력과 예측 사이의 인과 관계(모델이 블랙 박스로만 보일 경우)입니다. 입력은 예측을 유발합니다(데이터의 실제 인과 관계를 반영할 필요는 없음).
실제로 예측되는 입력과 결과 사이의 관계가 인과관계가 아닐지라도, 우리는 예측의 원인으로 모델의 입력을 볼 수 있습니다.
이 간단한 그래프를 고려할 때, 실제로 예측되는 입력과 결과 사이의 관계가 인과관계가 아닐지라도, 우리는 예측의 원인으로 모델의 입력을 볼 수 있습니다.
이 간단한 그래프를 통해 기계 학습 모델의 예측을 위해 어떻게 반사실적 요소를 시뮬레이션할 수 있는지 쉽게 알 수 있습니다. 예측하기 전에 인스턴스의 피쳐 값을 변경하기만 하면 예측이 어떻게 변경되는지 분석할 수 있습니다. 우리는 예측 등급의 전환(예: 승인 또는 거부)이나 예측이 특정 임계값에 도달하는 시나리오(예: 암 발생 확률은 10%에 도달하는 경우)와 같은 적절한 방식으로 예측이 변화하는 시나리오에 관심이 있습니다. 예측에 대한 반사실적 설명은 예측을 사전 정의된 출력으로 변경하는 피쳐 값의 가장 작은 변화를 설명합니다.
반사실적 설명 방법은 모델 입력 및 출력에서만 작동하므로 모델에 구애받지 않습니다. 해석은 형상값의 차이를 요약한 것으로 표현할 수 있기 때문에 모델에 구애받지 않는 장에서도 편안함을 느낄 수 있습니다(“예측을 변경하기 위해 기능 A와 B 변경”). 그러나 반사실적 설명은 그 자체가 새로운 예이므로, 이 장(“예: X에서 시작하여 A와 B를 변경하여 반사실적 인스턴스를 얻음)”에 수록된다. 프로토타이프와 달리, 반사실적 요소가 교육 데이터의 실제 사례일 필요는 없지만, 기능 값의 새로운 조합이 될 수 있습니다.
반사실적 요소를 만드는 방법에 대해 토론하기 전에, 저는 반사실적 사용에 대한 몇 가지 사례와 어떻게 좋은 반사실적 설명이 어떻게 보이는지에 대해 토론하고 싶습니다.
이 첫 번째 예에서 Peter는 대출을 신청하고 (기계 학습 동력이 있는) 은행 소프트웨어에 의해 거절당합니다. 그는 왜 그의 신청이 거절당했는지, 그리고 그가 대출을 받을 기회를 어떻게 개선할 수 있을지 궁금해 합니다. “why”라는 문제는 반사실적 질문으로 공식화할 수 있습니다. 예측을 거부에서 승인됨으로 변경하는 기능(소득, 신용카드 수, 연령 등)의 가장 작은 변화는 무엇입니까? 한 가지 가능한 대답은 다음과 같습니다. 만약 피터가 연간 10,000유로를 더 벌게 된다면, 그는 대출을 받을 것입니다. 또는 만약 피터가 신용카드를 적게 가지고 있고 5년 전에 대출금을 체납하지 않았다면, 그는 대출을 받을 것입니다. 피터는 은행이 투명성에 관심이 없기 때문에 거절의 이유를 결코 알 수 없을 것입니다. 하지만 그것은 또 다른 이야기입니다.
두 번째 예제에서는 반사실적 설명으로 연속적인 결과를 예측하는 모델을 설명하고자 합니다. 애나는 아파트를 임대하고 싶지만, 얼마를 내야 할지 잘 모르기 때문에, 집세를 예측하는 기계 학습 모델을 훈련시키기로 결심합니다. 물론, Anna는 데이터 과학자이기 때문에, 그것이 그녀의 문제를 해결하는 방법이다. 크기, 위치, 애완동물 허용 여부 등에 대한 모든 세부 사항을 입력한 후 모델에게 900유로를 충전할 수 있다고 말합니다. 그녀는 1000유로 이상을 기대했지만, 그녀의 모델을 신뢰하고 아파트의 가치를 향상시킬 수 있는 방법을 보기 위해 아파트의 특징적인 가치들을 가지고 놀기로 결심했습니다. 그녀는 아파트가 15m^5^ 더 크면 1000유로 이상 빌릴 수 있다는 것을 알게 되었습니다. 흥미롭지만, 행동할 수 없는 지식입니다. 왜냐하면 그녀는 아파트를 확장할 수 없기 때문입니다. 마지막으로, 자신의 통제 하에 있는 기능 값만 조정함으로써(예/아니요, 애완동물은 예/아니요, 바닥 유형 등) 그녀는 애완동물을 허용하고 더 나은 단열재로 창문을 설치하면 1000유로를 충전할 수 있다는 것을 알게 됩니다. Anna는 결과를 바꾸기 위해 반사실들과 직관적으로 일했습니다.
반사실성은 인간 친화적인 설명으로, 현재의 사례와는 대조적이고 선택적이기 때문에, 보통 소수의 특징적 변화에 초점을 맞춘다는 의미이다. 그러나 반사실주의자들은 ‘라쇼몬 효과’에 시달립니다. 라쇼몬은 사무라이의 살인사건을 다른 사람들에 의해 전해지는 일본의 영화이다. 각각의 이야기는 결과를 똑같이 잘 설명하지만, 이야기는 서로 모순됩니다. 반사실적 설명에도 동일한 현상이 발생할 수 있습니다. 대개의 경우 반사실적 설명이 여러 개 존재하기 때문입니다. 각 반사실들은 어떤 결과가 어떻게 도달했는지에 대해 다른 “이야기”를 말합니다. 한 반사실에서는 형상 A를 변경하라고 말할 수 있고, 다른 반사실에서는 형상 B를 동일하게 남겨두라고 말할 수 있는데, 이것은 모순입니다. 다중 진실의 이 문제는 모든 반사실적 설명을 보고하거나 반사실적 요소를 평가하고 최선의 진리를 선택하는 기준을 갖는 것으로 해결할 수 있습니다.
기준 얘기가 나와서 말인데, 어떻게 하면 좋은 반사실적 설명을 정의할 수 있을까요?
Generating Counterfactual Explanations
반사실적 설명을 생성하는 단순하고 순진한 접근 방식은 시행착오를 통해 검색하는 것입니다. 이 접근 방식에는 관심 인스턴스의 피쳐 값을 임의로 변경하고 원하는 출력이 예측될 때 중지하는 작업이 포함됩니다. 예를 들어 안나가 임대료를 더 낼 수 있는 아파트 버전을 찾으려고 했던 사례처럼 말이죠. 하지만 시행착오보다 더 나은 방법이 있습니다. 첫째, 관심의 인스턴스(instance)와 반사실적(repactual) 및 원하는(반사실적) 결과를 입력하는 손실 함수를 정의합니다. 손실은 반사실적 예측 결과가 사전 정의된 결과에서 얼마나 멀리 떨어져 있는지, 그리고 관심 사례에서 반사실적 결과가 얼마나 멀리 떨어져 있는지를 측정합니다. 최적화 알고리즘을 사용하거나 “Growing Spoes” 방법에 제시된 대로 인스턴스를 검색하여 손실을 직접 최적화할 수 있습니다(소프트웨어 및 대체.
이 섹션에서는 Wachter et al. (2017)1에서 제안하는 접근법을 설명하겠습니다. 그들은 다음과 같은 손실을 최소화할 것을 제안합니다.
\[L(x,x^\prime,y^\prime,\lambda)=\lambda\cdot(\hat{f}(x^\prime)-y^\prime)^5+d(x,x^\prime)\]첫 번째 항은 반사실적 x’의 모델 예측과 원하는 결과 y’ 사이의 2차 거리이며, 사용자는 이를 미리 정의해야 한다. 두 번째 항은 설명할 인스턴스 x와 반사실 x’ 사이의 거리이지만 나중에 이에 대해 더 자세히 설명합니다. $\lambda$ 매개 변수는 형상 값의 거리(두 번째 항)와 예측 거리(첫 번째 항)의 균형을 맞춥니다. 손실액은 지정된 $\lambda$에 대해 해결되며 반사실적 x’를 반환합니다. $\lambda$가 높을수록 원하는 결과 y에 가까운 반사실적 요소를 선호합니다. 값이 낮을수록 형상값의 x와 매우 유사한 반사실적 x’를 선호합니다. $\lambda$이(가) 매우 큰 경우 x에서 얼마나 떨어져 있든 간에 y’에 가장 가까운 예측이 있는 인스턴스가 선택됩니다. 궁극적으로, 사용자는 반사실적 예측이 원하는 결과와 일치한다는 요구 조건과 반사실적 예측이 x와 유사하다는 요구 조건의 균형을 어떻게 맞출지를 결정해야 합니다. 이 방법의 작성자는 $\lambda$에 대한 값을 선택하는 대신 반사실적 인스턴스의 예측이 y’에서 얼마나 멀리 허용되는지 허용된 공차 $\epsilon$를 선택할 것을 제안합니다. 이 제약 조건은 다음과 같이 쓸 수 있습니다.
\[|\hat{f}(x^\prime)-y^\prime|\leq\epsilon\]이 손실 기능을 최소화하기 위해 Nelder-Mead와 같은 모든 적절한 최적화 알고리즘을 사용할 수 있습니다. 기계 학습 모델의 구배에 액세스할 수 있는 경우 ADAM과 같은 구배 기반 방법을 사용할 수 있습니다. 설명해야 할 인스턴스 x, 원하는 출력 y’ 및 공차 매개 변수 $\epsilon$을(를) 미리 설정해야 합니다. 손실 기능은 x’에 대해 최소화되고 (현지) 최적의 반사실적 x’가 반환되는 동시에 충분히 가까운 해결책이 발견될 때까지 $\lambda$를 증가시킵니다(= 공차 파라미터 내에서).
\[\arg\min_{x^\prime}\max_{\lambda}L(x,x^\prime,y^\prime,\lambda)\]인스턴스(instance) x와 반사실적 x’ 사이의 거리를 측정하기 위한 함수 d는 역중위수 절대편차(MAD)를 사용하여 맨해튼 거리 가중치 형상을 시계방향으로 측정합니다.
\[d(x,x^\prime)=\sum_{j=1}^p\frac{|x_j-x^\prime_j|}{MAD_j}\]총 거리는 모든 p 형상의 거리, 즉 인스턴스 x와 반사실적 x’ 사이의 형상 값의 절대적 차이를 합한 값입니다. 형상의 거리는 다음과 같이 정의된 데이터 세트에서 형상 j의 중위수 절대 편차의 역순으로 조정됩니다.
\[MAD_j=\text{median}_{i\in{}\{1,\ldots,n\}}(|x_{i,j}-\text{median}_{l\in{}\{1,\ldots,n\}}(x_{l,j})|)\]벡터의 중위수는 벡터 값의 절반은 크고 나머지 절반은 작은 값입니다. MAD는 형상의 분산과 동일하지만 평균을 중심으로 사용하고 제곱 거리를 합하는 대신 중위수를 중심으로 사용하고 절대 거리에 걸쳐 합계를 사용합니다. 제안된 거리 함수는 간격성을 도입하는 유클리드 거리보다 유리합니다. 즉, 더 적은 피쳐가 다를 때 두 점이 서로 더 가깝다는 뜻입니다. 그리고 그것은 특이치에 더 강합니다. MAD를 이용한 축척은 모든 특징들을 동일한 규모로 만들기 위해 필요합니다. 아파트 크기를 평방 미터로 측정하든 평방 피트 단위로 측정하든 상관 없습니다.
반사실 제작 방법은 간단합니다.
- 설명할 인스턴스 x, 원하는 결과 y, 공차 $\epsilon$ 및 $\lambda$에 대한 (낮은) 초기 값을 선택합니다.
- 랜덤 인스턴스를 초기 반사실적으로 샘플링합니다.
- 초기 샘플링된 반사실성을 시작점으로 하여 손실을 최적화합니다.
-
$ \hat{f}(x^\prime)-y^\prime >\epsilon$: - $\lambda$을(를) 늘립니다.
- 현재 반사실적 방법으로 시작점으로 손실을 최적화합니다.
- 손실을 최소화하는 반사실성을 반환합니다.
- 2-4단계를 반복하고 상실을 최소화하는 반사실 또는 상실의 목록을 반환합니다.
예시
두 가지 예는 모두 Wachter 등(2017년)의 작업에서 가져온 것입니다.
첫 번째 예에서, 저자들은 로스쿨의 1학년 평균점수, 인종, 로스쿨 입학 시험 점수에 기초하여 로스쿨의 1학년 평균 성적을 예측하기 위해 완전히 연결된 3단 신경망을 훈련합니다. 목표는 다음 질문에 답하는 각 학생에 대한 반사실적 설명을 찾는 것입니다. 예측 점수 0을 얻으려면 입력 기능을 어떻게 변경해야 합니까? 이전에 점수가 정규화된 적이 있기 때문에, 0점을 받은 학생은 학생들의 평균점수만큼 우수합니다. 음수는 평균보다 낮은 결과, 양수는 평균보다 높은 결과를 의미합니다.
다음 표는 학습된 반사실 관계를 보여 줍니다.
| Score | GPA | LSAT | Race | GPA x’ | LSAT x’ | Race x’ |
|---|---|---|---|---|---|---|
| 0.17 | 3.1 | 39.0 | 0 | 3.1 | 34.0 | 0 |
| 0.54 | 3.7 | 48.0 | 0 | 3.7 | 32.4 | 0 |
| -0.77 | 3.3 | 28.0 | 1 | 3.3 | 33.5 | 0 |
| -0.83 | 2.4 | 28.5 | 1 | 2.4 | 35.8 | 0 |
| -0.57 | 2.7 | 18.3 | 0 | 2.7 | 34.9 | 0 |
첫 번째 열에는 예측 점수, 다음 세 열에는 원래 피쳐 값, 마지막 세 열에는 0에 가까운 점수가 나오는 반사실적 피쳐 값이 포함됩니다. 처음 두 행은 평균 이상의 예측을 가진 학생이고, 나머지 세 행은 평균보다 낮습니다. 처음 두 행에 대한 반사실적 설명에서는 예측 점수를 낮추기 위해 학생의 특징이 어떻게 변화해야 하는지, 그리고 나머지 세 경우 평균 점수를 높이기 위해 어떻게 변화해야 하는지 설명합니다. 점수를 늘리기 위한 반작용제에서는 항상 레이스를 검정색(1로 코드화됨)에서 흰색(0으로 코드화됨)으로 변경하여 모델의 인종적 편향을 보여줍니다. 반사실상 GPA는 변경되지 않지만 LSAT는 변경됩니다.
두 번째 예는 당뇨병의 위험 예측에 대한 반사실적 설명을 보여줍니다. 완전히 연결된 3단 신경망은 연령, BMI, 임신 횟수 등에 따라 피마 유산의 여성에 따라 당뇨병의 위험을 예측하도록 훈련됩니다. 이에 대한 반사실적 답변은 다음과 같습니다. 당뇨병의 위험 점수를 0.5로 늘리거나 낮추려면 어떤 특징 값을 변경해야 합니까? 다음과 같은 반사실적 요소가 발견되었습니다.
- Person 1: 2시간 혈청 인슐린 수치가 154.3이라면 0.51점입니다.
- Person 2: 2시간 혈청 인슐린 수치가 169.5였다면 0.51점입니다.
- Person 3: 혈장 포도당 농도가 158.3이고 혈청 인슐린 수치가 160.5였다면 0.51점입니다.
장점
반사실적 설명의 해석은 매우 명확합니다. 반사실성에 따라 인스턴스(instance)의 피쳐 값이 변경되면 예측이 미리 정의된 예측으로 변경됩니다. 배경에는 추가적인 가정도 없고 마법도 없습니다. 이것은 또한 LIME와 같은 방법만큼 위험하지 않다는 것을 의미하며, 여기서 해석을 위해 로컬 모델을 얼마나 멀리 추정할 수 있는지 불분명합니다.
반사실적 방법은 새 인스턴스를 만들지만 변경된 형상 값을 보고하여 반사실적 요약을 요약할 수도 있습니다. 이를 통해 *** 결과를 보고할 수 있는 두 가지 옵션이 제공됩니다. 반사실적 인스턴스를 보고하거나 관심 인스턴스와 반사실적 인스턴스 간에 변경된 기능을 강조 표시할 수 있습니다.
반사실적 방법은 데이터 또는 모델에 대한 액세스가 필요하지 않습니다. 예를 들어 웹 API를 통해 작동하는 모델의 예측 기능에만 액세스하면 됩니다. 이는 타사에서 감사를 받거나 모델이나 데이터를 공개하지 않고 사용자에게 설명을 제공하는 기업에게 매력적입니다. 기업은 영업 기밀 또는 데이터 보호 이유로 모델과 데이터를 보호하는 데 관심이 있습니다. 반사실적 설명은 모델 예측을 설명하는 것과 모델 소유자의 이익을 보호하는 것 사이의 균형을 제공합니다.
** 메서드는 기계 학습**을 사용하지 않는 시스템에서도 작동합니다. 입력을 수신하고 출력을 반환하는 모든 시스템에 대해 반사실 관계를 생성할 수 있습니다. 아파트 임대료를 예측하는 시스템도 손으로 쓴 규칙으로 구성될 수 있고, 반사실적 설명도 여전히 효과가 있을 것입니다.
반사실적 설명 방법은 표준 최적화 도구 라이브러리로 최적화할 수 있는 손실 기능이기 때문에 비교적 쉽게 구현할 수 있습니다. 피쳐 값을 유의한 범위로 제한(예: 양수 아파트 크기만)하는 등 일부 추가 세부 정보를 고려해야 합니다.
단점
각 인스턴스에 대해 일반적으로 여러 개의 반사실적 설명(Rashomon effect)을 찾을 수 있습니다. 이것은 불편합니다. 대부분의 사람들은 현실 세계의 복잡성보다 간단한 설명을 선호합니다. 그것은 또한 현실적인 도전입니다. 한 가지 사례에 대해 23가지 반사실적 설명을 생성했다고 가정하겠습니다. 다 보고하는 건가요? 최고만요? 만약 그들이 모두 비교적 “좋지만” 매우 다르다면 어떨까요? 이 질문들은 각 프로젝트에 대해 새롭게 답해야 합니다. 여러 가지 반사실적 설명을 하는 것도 유리할 수 있습니다. 그러면 인간은 이전의 지식에 상응하는 것을 선택할 수 있기 때문입니다.
지정된 공차 $\epsilon$에 대해 반사실적 인스턴스가 발견된다는 보장은 없습니다**. 그것은 반드시 방법의 잘못이 아니라 데이터에 따라 다릅니다.
제안된 방법 *는 다양한 수준의 범주형 피쳐를 잘 처리하지 않습니다. 메소드의 작성자는 범주형 피쳐 값의 각 조합에 대해 이 방법을 별도로 실행할 것을 제안했지만, 많은 값을 가진 여러 범주형 피쳐가 있는 경우 조합형 폭발을 일으킵니다. 예를 들어, 10개의 고유 레벨을 가진 6개의 범주형 피쳐는 100만 번의 실행을 의미합니다. 범주형 기능만을 위한 해결책은 Martens et al. (2014)2에 의해 제안되었습니다. 범주형 변수에 대한 동요를 생성하기 위한 원칙적인 방법으로 수치 및 범주형 변수를 모두 처리하는 솔루션은 Python 패키지 Alibi)에서 구현됩니다.
소프트웨어 및 대안책
반사실적 설명은 Python 패키지 Alibi)에서 구현됩니다. 패키지 작성자는 단순한 반사실적 방법)과 확장된 방법)을 구현하여 알고리즘 출력의 해석성과 수렴성을 향상시킵니다3.
문서 분류를 설명하기 위해 매우 유사한 접근법이 Martens 등(2014년)에 의해 제안되었습니다. 그들의 작품에서, 그들은 왜 문서가 특정 클래스로 분류되었는지 또는 분류되지 않았는지를 설명하는 데 초점을 맞춥니다. 이 장에서 제시된 방법의 차이점은 Martens 등(2014)이 입력 단어로 단어 발생을 갖는 텍스트 분류기에 초점을 맞춘다는 것입니다.
반사실들을 검색하는 다른 방법은 Laugel et al. (2017)4에 의한 성장하는 구 알고리즘입니다. 이 방법은 먼저 관심 지점 주위에 구를 그리고, 해당 구 내의 점을 샘플링하고, 샘플링된 점 중 하나가 원하는 예측을 산출하는지, (비교) 반사실체를 찾아 최종적으로 반환할 때까지 구를 수축시키는지 또는 그에 따라 구를 확장하는지 확인합니다. 그들은 논문에 반사실이라는 단어를 사용하지 않지만, 그 방법은 상당히 비슷합니다. 또한 형상 값의 변경이 가능한 적은 반사실적 요소를 선호하는 손실 함수를 정의합니다. 기능을 직접 최적화하는 대신, 구를 사용한 위에서 언급한 검색을 제안합니다.

그림 6.2: Laugel et al. (2017)에 의해 구가 성장하고 희박한 반사실들을 선택하는 것을 보여주는 그림입니다.
리베이루 외 (2018)5에 의한 앵커는 반사실상의 반대이다. 질문에 대한 앵커의 답변은 다음과 같습니다. 예측을 고정하기에 충분한 피쳐, 즉 다른 피쳐를 변경해도 예측을 변경할 수 없는 피쳐는 무엇입니까? 예측을 위한 앵커 역할을 하는 피쳐를 찾으면 앵커에서 사용되지 않는 피쳐를 변경하여 더 이상 반사실적 인스턴스를 찾을 수 없습니다.

그림 6.3: 리베이루 외(2018년)에 의한 앵커의 예이다.
-
Wachter, Sandra, Brent Mittelstadt, and Chris Russell. “Counterfactual explanations without opening the black box: Automated decisions and the GDPR.” (2017). ↩
-
Martens, David, and Foster Provost. “Explaining data-driven document classifications.” (2014). ↩
-
Van Looveren, Arnaud, and Janis Klaise. “Interpretable Counterfactual Explanations Guided by Prototypes.” arXiv preprint arXiv:1907.02584 (2019). ↩
-
Laugel, Thibault, et al. “Inverse classification for comparison-based interpretability in machine learning.” arXiv preprint arXiv:1712.08443 (2017). ↩
-
Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin. “Anchors: High-precision model-agnostic explanations.” AAAI Conference on Artificial Intelligence (2018). ↩